I never thought of this problem before - need clarification.. Mostly a mind-thought exercise, so no need to go nuts. 
Does the internal resistance of a single cell ALSO need to include the internal resistance of any cells prior to it?
I'll start out with a perfect-world scenario:
I have simple 4S battery, where each cell is exactly equal to each other in both capacity and internal resistance. Let's say cell interlinks are zero, for the sake of argument. Let's say the internal resistance of a single cell is 2 milliohm.
So, during operation, is it something like this during charge and discharge:
Cell 1 IR = 2 milliohm
Cell 2 IR = 4 milliohm (cell 1 and itself)
Cell 3 IR = 6 milliohm (cell 1, 2, and itself)
Cell 4 IR = 8 milliohm (cell 1, 2, 3, and itself)
My mind is reeling. If that is the case, then even bottom-balancing is no guarantee of hitting the same voltage at the same time *in the lab-perfect world*, under discharge. Bottom balancing procedure involves *resting voltages* of individual cells, and not an in-series *discharge / charge voltage*. Maybe it is so small it doesn't matter. I don't have a high-current application, so I haven't seen major differences when bottom-balancing where this kind of IR-differential under working conditions matter, but still wonder, especially with long strings, like one might have with a 48v bank?
Would the lab-perfect solution be to manufacture each successive cell with different IR values to compensate, or more easily manufacture each cell with a slightly different capacity to compensate for the differences in IR? Of course each cell would have to be positioned properly. This is a thought-question, and not real-world obviously.
Or am I just thinking outside the box (er, butt most likely.)
Does the internal resistance of a single cell ALSO need to include the internal resistance of any cells prior to it?
I'll start out with a perfect-world scenario:
I have simple 4S battery, where each cell is exactly equal to each other in both capacity and internal resistance. Let's say cell interlinks are zero, for the sake of argument. Let's say the internal resistance of a single cell is 2 milliohm.
So, during operation, is it something like this during charge and discharge:
Cell 1 IR = 2 milliohm
Cell 2 IR = 4 milliohm (cell 1 and itself)
Cell 3 IR = 6 milliohm (cell 1, 2, and itself)
Cell 4 IR = 8 milliohm (cell 1, 2, 3, and itself)
My mind is reeling. If that is the case, then even bottom-balancing is no guarantee of hitting the same voltage at the same time *in the lab-perfect world*, under discharge. Bottom balancing procedure involves *resting voltages* of individual cells, and not an in-series *discharge / charge voltage*. Maybe it is so small it doesn't matter. I don't have a high-current application, so I haven't seen major differences when bottom-balancing where this kind of IR-differential under working conditions matter, but still wonder, especially with long strings, like one might have with a 48v bank?
Would the lab-perfect solution be to manufacture each successive cell with different IR values to compensate, or more easily manufacture each cell with a slightly different capacity to compensate for the differences in IR? Of course each cell would have to be positioned properly. This is a thought-question, and not real-world obviously.
Or am I just thinking outside the box (er, butt most likely.)

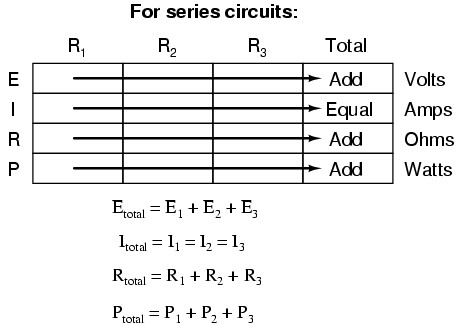

Comment